最高のコレクション 三平��の定理 証明 円 338217-三平���の定理 証明 円

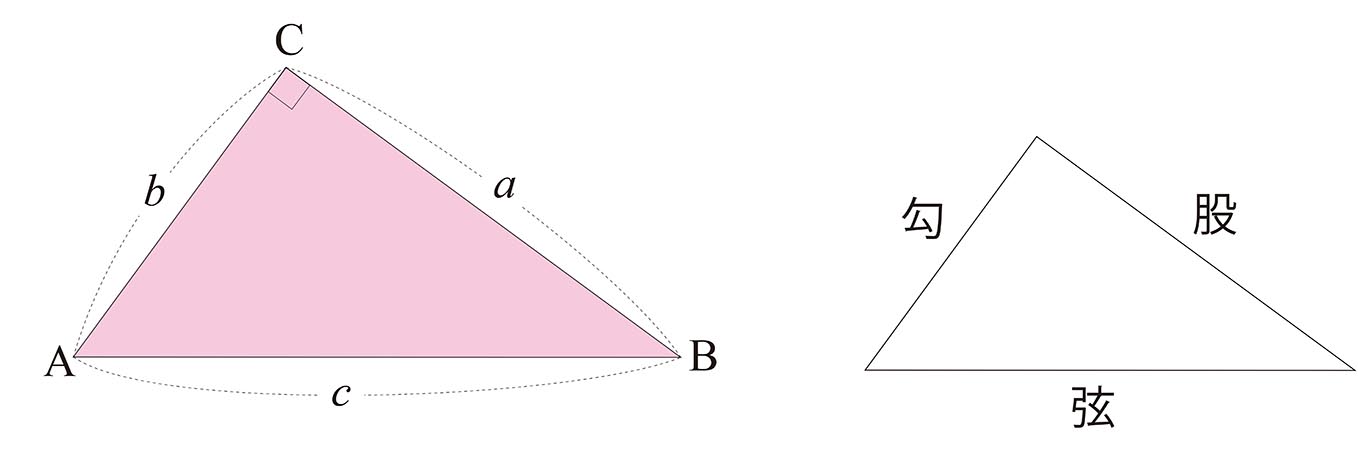
三平方の定理と円 例題 弦ABの長さを求める。 円Oの半径6cm、中心から弦ABまでの距離が2cmである。 A B O 半径6cm 2cm 円Oに点Pから引いた接線PAの長さを求める。 円Oの半径5cm、OP=10cm、Aは接点である。 A P O 半径5cm, OP=10cm ① 直角三角形AOPで三平方の定理を三平方の定理の証明⑬（外接円と直角二等辺三角形を利用した 三平方の定理の証明 三平方の定理は、数百通りともいわれる証明法が提案されている。よく目にする証明法は、正方形を用いた証明、相似を用いた証明、内接円を用いた証明などがあります。 三平方の定理の証明 三平方の定理とは以下のように直角三角形ABCがあった時に、辺a（底辺）と辺b（高さ）の2つと辺c（斜辺）の関係性を以下のような等式で表した定理です。 公式：a²＋b²＝c² わかりやすく文章で表現しますと、 底辺の2乗と高さの2乗の

三平方の定理の逆 Youtube

三平方の定理 証明 円

三平方の定理 証明 円-4 三平方の定理の応用問題 14 右の図のように，線分 ab を直径とする円oの周上に点cをとる。 ∠cab の二等分線と線分 cb の交点をdとし，点dから線分 ab に 垂線をひき，その交点をeとする。次の問いに答えよ。 ⑴ acd≡ aed となることを証明せよ。三平方の定理はいたるところで活躍している。 超難問マイクロソフトの入社試験で書いた問題 下の図の直角三角形の面積を求めよ。 これも三平方の定理を使うのだけれど・・ ということで、今回は三平方の定理の証明をしてみる。 1． 三平方の定理の証明

中学数学 円周率は3より大きいの証明 数樂管理人のブログ

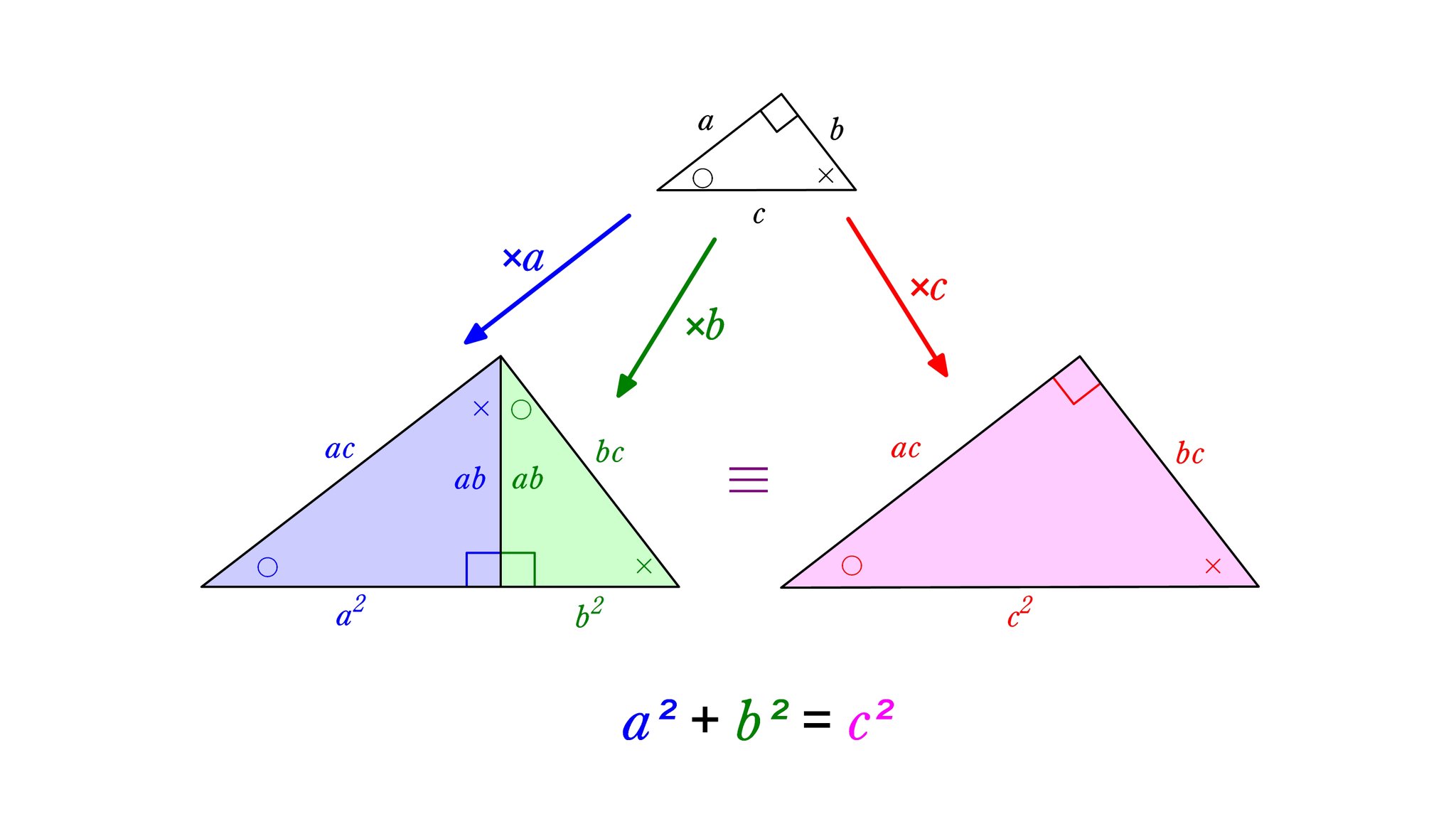
 三平方の定理 といいます。 ピタゴラスの定理という名称もありますが、 私はピタゴラスが発見したとは思っていないので 三平方の定理としておきます。 それでは以下で 三平方の定理 を証明していきたいと思います。 今回は余弦定理の証明の前振りにあとは、三平方の定理で解決します。 ここで、計算を簡単にするために、 y = 1 y = 1 のときの相似な三角形で長さを求めましょう。 三角形 AEH A E H に三平方の定理を使うと、 AE = √10 A E = 10 なので、 これは、本来の図と相似比が 8 √10 8 10 です。 三角形 中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 私立高校入試対策 公立高校入試対策 式の展開式の展開の基

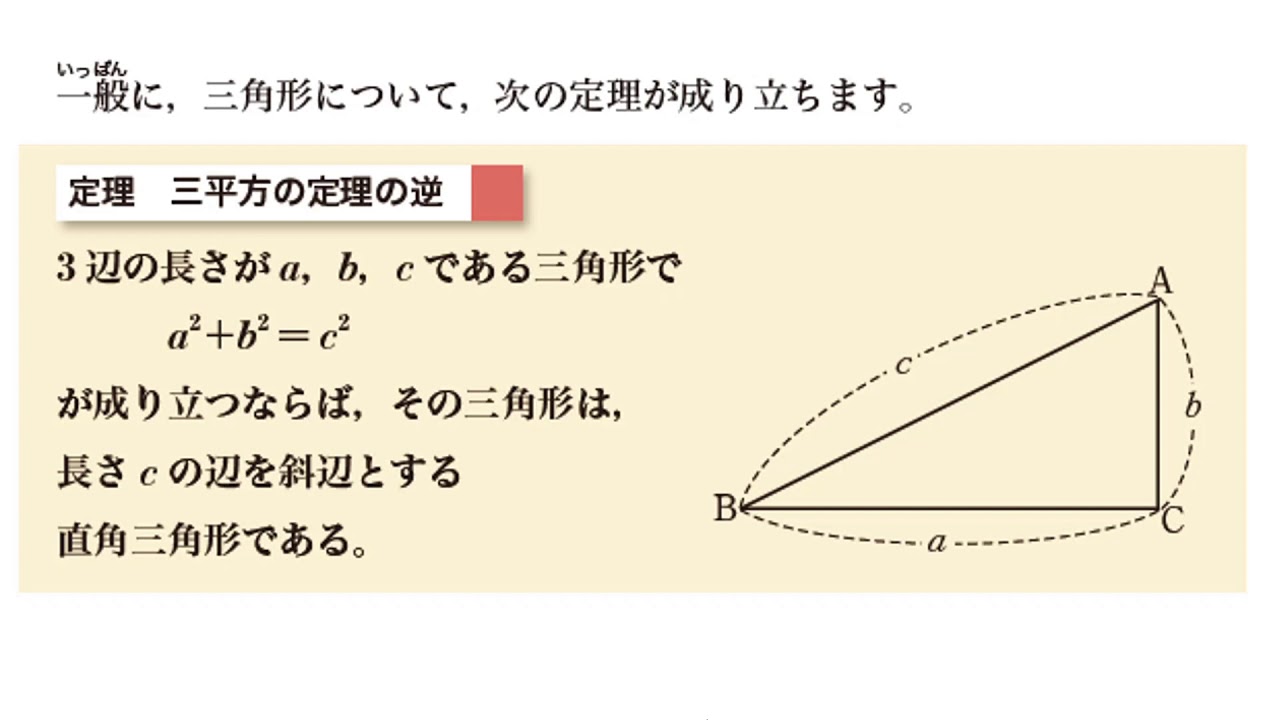
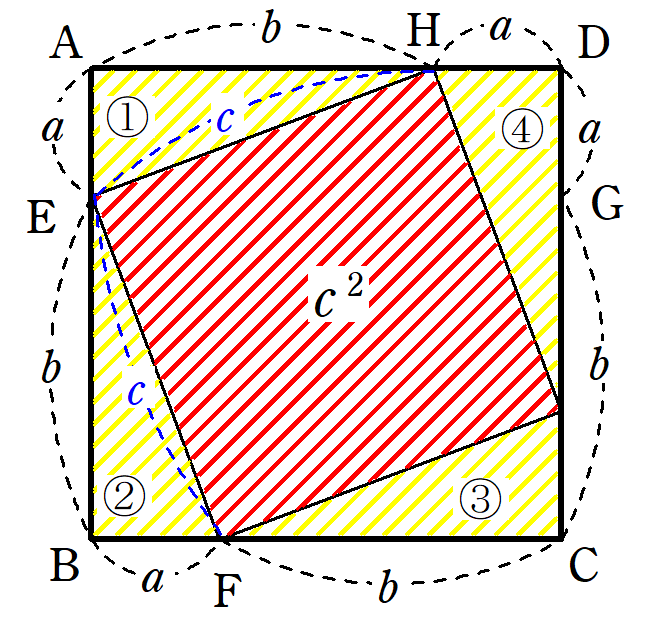
三平方の定理の追加証明3 三平方の定理の証明＜8＞(秋山仁先生NHK高校講座「数学基礎」) c を1 辺とする正方形の面積から ①，③，B を 赤枠の中に移動する c 2＝a ＋b 三平方の定理の証明＜9＞ 赤い線と青い線が一致するように ①～⑤の図形を移動する a b b B 3 三平方の定理を使った証明 （1）点 \(A\) が円 \(O\) の内部にある場合 点 \(A\) を通る任意の直線が円 \(O\) と交わる点を \(P,Q\) とすると \(AP\cdot AQ\) は一定である。*2 方べきの定理を三平方の定理を使って証明します。 ピタゴラスの定理とその証明 逆はこちらにあります 三平方の定理の逆 正弦定理 a 90°のとき abcの外接円oの中心をabが通るように、点aを円周上で移動させる。移動後の点をa'とする。 このとき∠a=∠a'(円周角の定理)。 a'bはoの直径なので∠a'cb=90°（ターレス

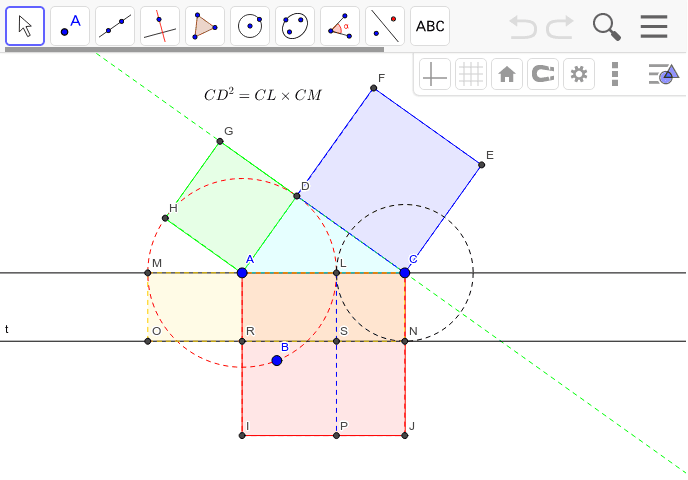
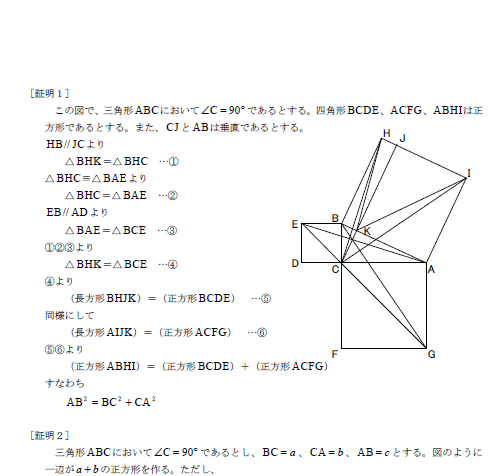
三平方の定理の証明 (ユークリッドの証明) 作成者 kageyama トピック 数学, 平面, ピタゴラスまたはピタゴラスの定理, 直角三角形40通りの三平方の定理の証明1です。 三平方の定理（ピタゴラスの定理）の証明pdf1の説明です。 榜接円・円の接線の性質と面積を利用した証明です。証明5と似ています。三平方の定理を使う平面図形の難問たち 三平方の定理を利用して三角形の高さを求める問題 次の図のような三角形ABCがあり、BC⊥AHである。 このとき、AHの長さを求めよ。 解説 答え： 5 2 √ 7 5 2 7 (㎝) ～ポイント～ 三平方の定理を使う、このパターン

3分で分かる 三平方の定理の公式と証明 使い方をわかりやすく 合格サプリ

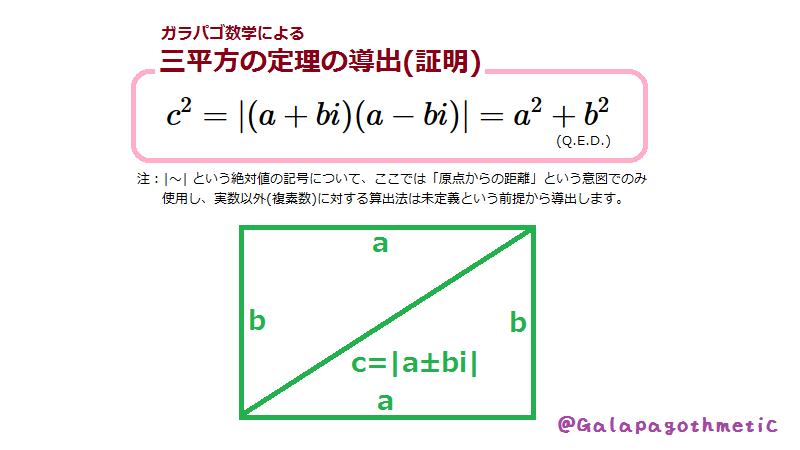
ガラパゴ数学 ますらば 三平方の定理の証明は数多く知られていますが これ以上にシンプルなものは存在するでしょうか 座標を 数 と捉えるガラパゴ数学にとって この定理の導出は避けて通れません 詳しい解説はリプ欄に貼りますので 是非ご覧

正弦定理の証明 外接円の半径Rを積極的に用いる証明 1 普通の証明（1） 2 垂線CHの長さに着目した証明 3 中心原点、半径Rの円を用いる方法 4 図形と式を用いる方法 「～ ～」は私の感想です ～無理やり円を作るところが不満～ ～見事！三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_2点間の距離 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離 三平方の定理の利用（円の接線） 前章・三平方の定理の利用（二点間の距離） 問1は線の引き方を知らないと苦労するタイプの問題だ。 OO',OA,OBと線を引き、さらに直角三角形を作るように線を引く。 こうすることにより、三平方の定理を利用できる

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

三平方の定理 証明１２ Geogebra

 三平方の定理を使って面積を求める方法は？ 問題を使って解説するよ！ 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に単元 三平方の定理 三角定規 15度 直角三角形 整数問題 証明問題 神奈川 平行四辺形 三平方の定理 円 直交する弦 相似 メネラウス 三平方の定理 神奈川 入試 平行線の錯角と同位角 循環小数・有理数・無限小数・41の倍数 中点連結定理 相似 内接円・外接円・三平方の定理 連立方程式 計算 三平方の定理の色々な証明を知りたいです。 証明が載っているリンクを色々教えてください。 お願いします。 あと、三平方の定理の証明は今まで知られているもので 全部でいくつあるの

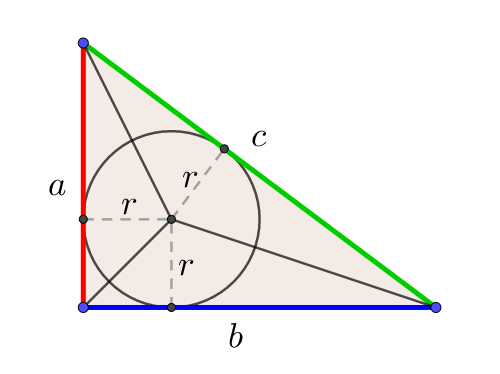
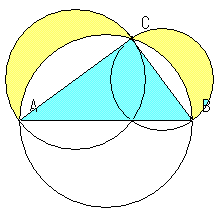
三平方の定理の証明 内接円を利用した証明方法をわかりやすく解説 面積と接線の性質をフル活用 Fukusukeの数学めも

中学3年数学 円と相似と三平方の定理の融合問題 赤城 ᐡᐤᐡ

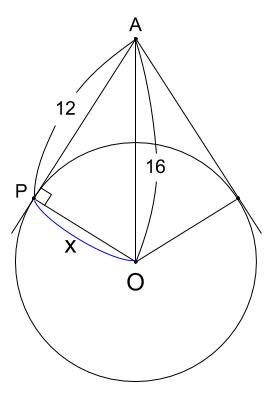
使う定理・法則 三平方の定理 wiki参照 三平方の定理とは、直角三角形の斜辺と 他の二辺の間に成り立つ超重要公式です。 上図を用いた式で表すと、 中3 三平方の定理 カテゴリーの記事一覧 すべて無料！ 星組の中学数学講座 授業動画は声と手だけ、テキストは下手な字で手書きの低クオリティー！ だけど、内容は役に立つと思います。 また、無料学習プリント集としてもお使いいただけます円外の点から円に接線を引くとき、左右対称な 2 2 本の接線が引けます。 どちらで解いても関係ないですね。 求める半径の長さを x x とすると 三平方の定理より x2 122 = 162 x 2 12 2 = 16 2 x2 144 = 256 x 2 144 = 256 x2 = 112 x 2 = 112 x = ±√112 x = ± 112 = ±4√7 = ± 4 7

三平方の定理の証明 ピタゴラスの証明の方法をわかりやすく解説 定理の本当の発見者はバビロニア人 Fukusukeの数学めも

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4

三平方の定理を直接証明するというものではないので、ややこしく感じるかもしれません。 納得できない人のために、次は図で直感的に理解できるよう解説します。 三平方の定理が直感的にわかる図 三平方の定理は各辺の2乗の等式です。森下四郎『ピタゴラスの定理100の証明法 幾何の散歩道』プレアデス出版、10年8月、改訂版。 isbn 。 森下四郎『ピタゴラスの定理をめぐる2つの謎 三平方の定理の謎』プレアデス出版、10年12月。 isbn 。 関連項目 数検1級 三角形と円を題材にして、大きく三角形の合同・三角形の相似・三平方の定理・円の性質を勉強するよ。 最後に行くにつれて簡単に感じると思いますが、数検対応級は 5級 ～ 準2級 です。 数学検定5級合格率75%！ 過去問は中学1年生範囲だ

1

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

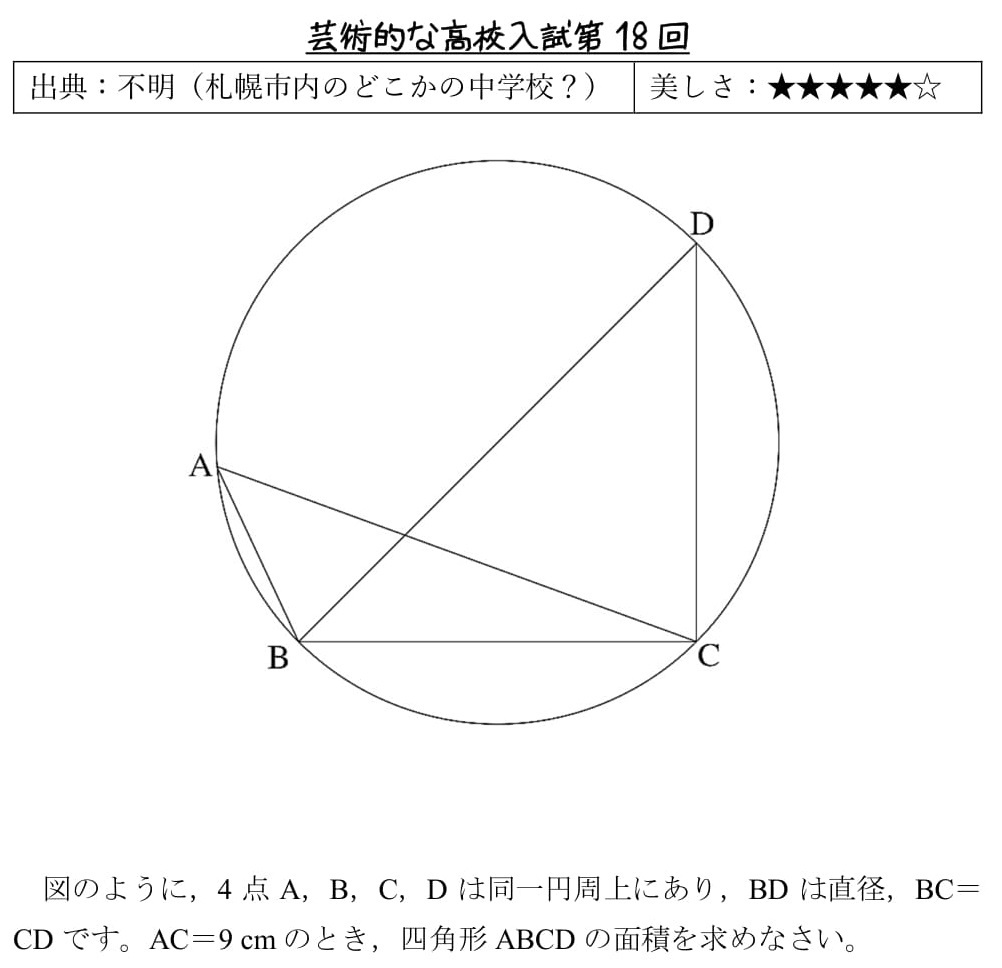
三平方の定理の証明 いろいろな種類40通りの証明を行いました。 丁寧とはいえない書き方のものもありますが、各自補って読んでください。 三角形や四角形の面積（等積変形など）を用いているもの、三角形の相似を用いているもの、 別の定理を証明し三平方の定理です 口 &同 ーールーーー、、 2 ABを直径とする円Oがある。 線分 ABのBを越える延長上に 点Pをとり,直線 PCが円Oの接線となるように, 円Oの周上に 点Cをとる。円0の半径をr, OP=d, PC=l とするとき, OPC について三平方の定理が成り立つことを証明し太郎 なので同じことですね． 南海 というより，三平方の定理から余弦定理に至る途中で経由する等式だ． 余弦定理は に関して対称な形をしているが， の入る等式は対称性が見えにくいので， いずれからの垂線がよいのか個別に考えなければならなかった． ． われわれは余弦定理を

三平方の定理の証明４ 直角三角形と内接円 キソカラ

ポテト一郎 三平方の定理 一番好きな証明です T Co Nkbjthkv Twitter

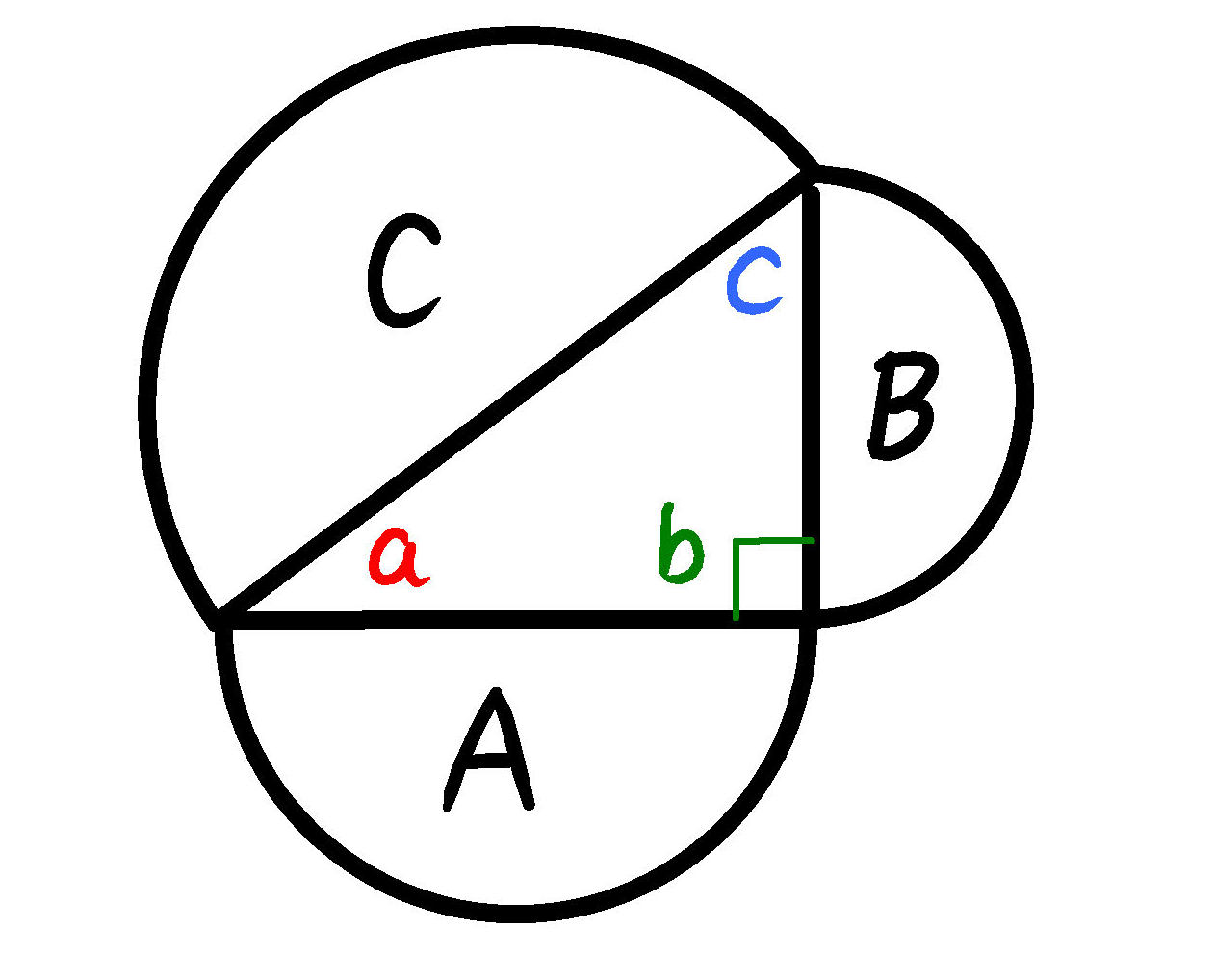
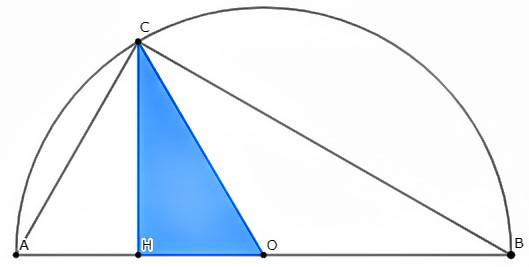
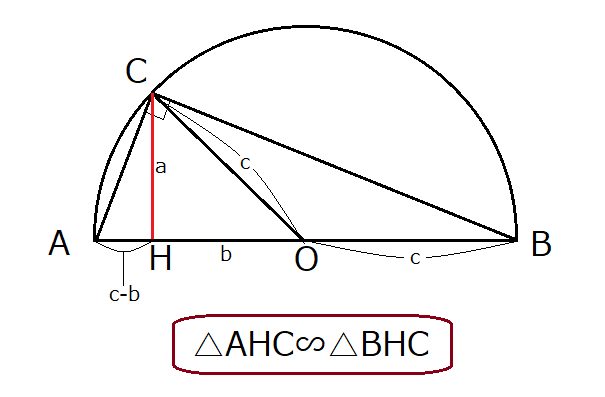
 トレミーの定理より「 上×下 ＋ 左×右 ＝対角線のかけ算」なので a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 となります。これは三平方の定理より，確かに成立していることがわかります（逆に，トレミーの定理を使うことで三平方の定理が証明できる，とも言え三平方の定理 ア 三平方の定理の意味と証明 三平方の定理(ピタゴラスの定理)！一度は聞いたことがあるのではないでしょうか まさに、『 King of 定理』と言えますね！ 単純なのにすごく役立つ 経済的に言えば「コストパフォーマンス」がよい、すごく 三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。 この記事では、 外接円と直角二等辺三角形を利用した証明方法 を、 現役数学教員がわかりやすく解説 します。 今回の証明は、 世紀後半～21世紀 にベトナム人の Bui Quang Tuan によって考案さ

三平方の定理の逆 Youtube

中3数学 円の中心と弦との距離 例題編 映像授業のtry It トライイット

 三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。 この記事では、その中でも 直角三角形の内接円の性質をフル活用した証明方法 について、 現役数学教員がわかりやすく解説 します。 計算が多い証明方法ではありますが、やっていることは明快。

三平方の定理を使った証明 Youtube

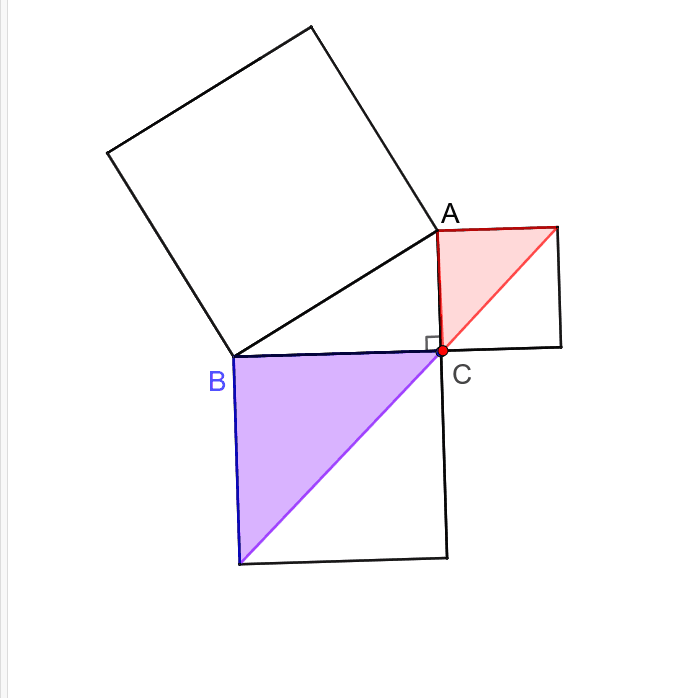
三平方の定理の証明 ユークリッドの証明 Geogebra

ピタゴラスの定理の証明 大栗博司のブログ

円の方程式の公式は 3分でわかる意味 求め方 証明 ３点を通る円の方程式

三平方の定理

円の方程式とは 3分でわかる意味 公式 半径との関係

コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

ベリースライム 五平方の定理 三平方の定理で示すことができます 見た目を重視して 円の直径をrとしています 数学 T Co Jkcttxf0tw Twitter

三平方の定理 ピタゴラスの定理 の証明

ピタゴラスの定理の簡単な証明方法ありますか Quora

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

ファイル 三平方の定理 Jpg Wikipedia

三平方の定理 直角三角形は少なくとも１辺は偶数である 証明 背理法練習問題 数学メモランダム

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

1

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

三平方の定理の４通りの美しい証明 高校数学の美しい物語

この計算できますか No 243 三平方の定理 証明 内接円 Youtube

三平方の定理およびその逆 証明 理数系学習サイト Kori

中学数学 三平方の定理の利用 円

ピタゴラスの定理の拡張のしかた

三平方の定理の４通りの美しい証明 高校数学の美しい物語

三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋all Rights Reserved

Dvd 高校入試数学シリーズ Dvdを見て攻略 全5巻 Dvd未開封 三平方の定理 いろいろな図形 関数とグラフ 方程式とその利用 数と式 高校受験 Pik2ar Org

三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

Many Proofs Of Pythagorean Theorem

3

円周角の定理を使った相似の証明の解き方 2 現役塾講師のわかりやすい中学数学の解き方

中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

三角比の導入 三平方の定理について 三平方の定理の証明方法は非常にたくさんある 等積変形を用いた証明法は以下の通り 下の画像をクリックすると動画が表示されます それでは 以下の図を利用して 三平方の定理の別証明を考えてみよう

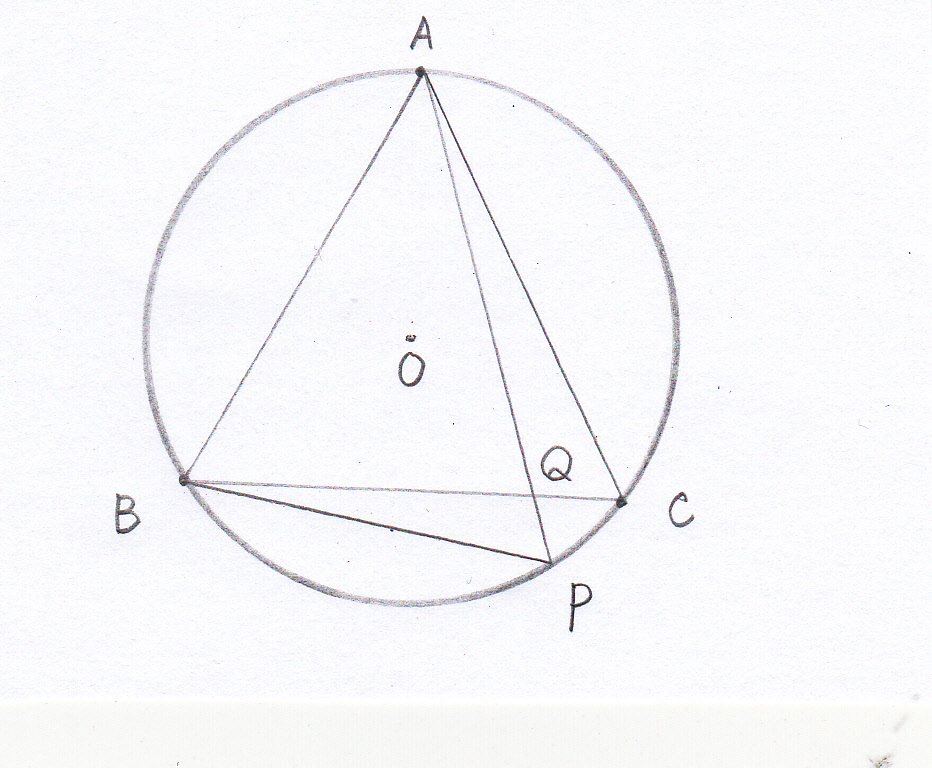
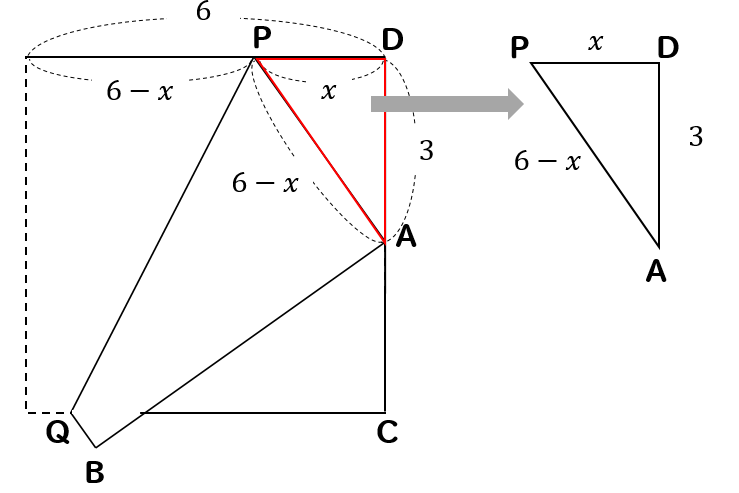
円周角と三平方 トレミーの定理が背景 高校入試 数学 良問 難問

数学を愛する会 三平方の定理の証明 物理 T Co Wwiir0hyal Twitter

三平方の定理で底辺の二乗と高さの二乗をたせば どう考えたって斜辺の二乗になるに決まってるじゃん ほらなと中坊に簡単にうなずかせて解らせる方法を教えて下さいますか Quora

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三石 数学塾 三平方の定理の証明 その２

理論編 三平方の定理 の復習 早大生の 省かない 数学

中学数学 円周率は3より大きいの証明 数樂管理人のブログ

三平方の定理 方程式を利用する発展問題を解説 数スタ

三平方の定理

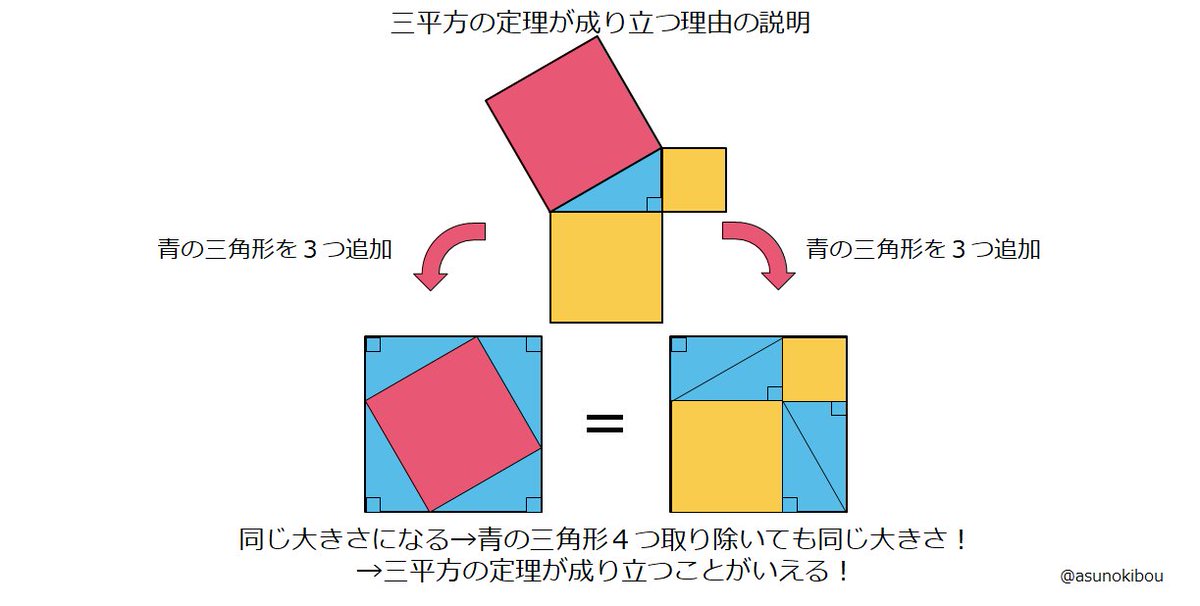
Twitter 上的 横山 明日希 三平方の定理が成り立つことの証明方法は数多く見つかっていますが 直観的に理解できるものを紹介しますね 紙で作ってみるとより感動できると思いますのでぜひやってみてください T Co C7qglpvmqo Twitter

三平方の定理の証明 Geogebra

三平方の定理 ピタゴラスの定理 の証明まとめ５選 全部でいくつあるの 遊ぶ数学

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 トムラボ

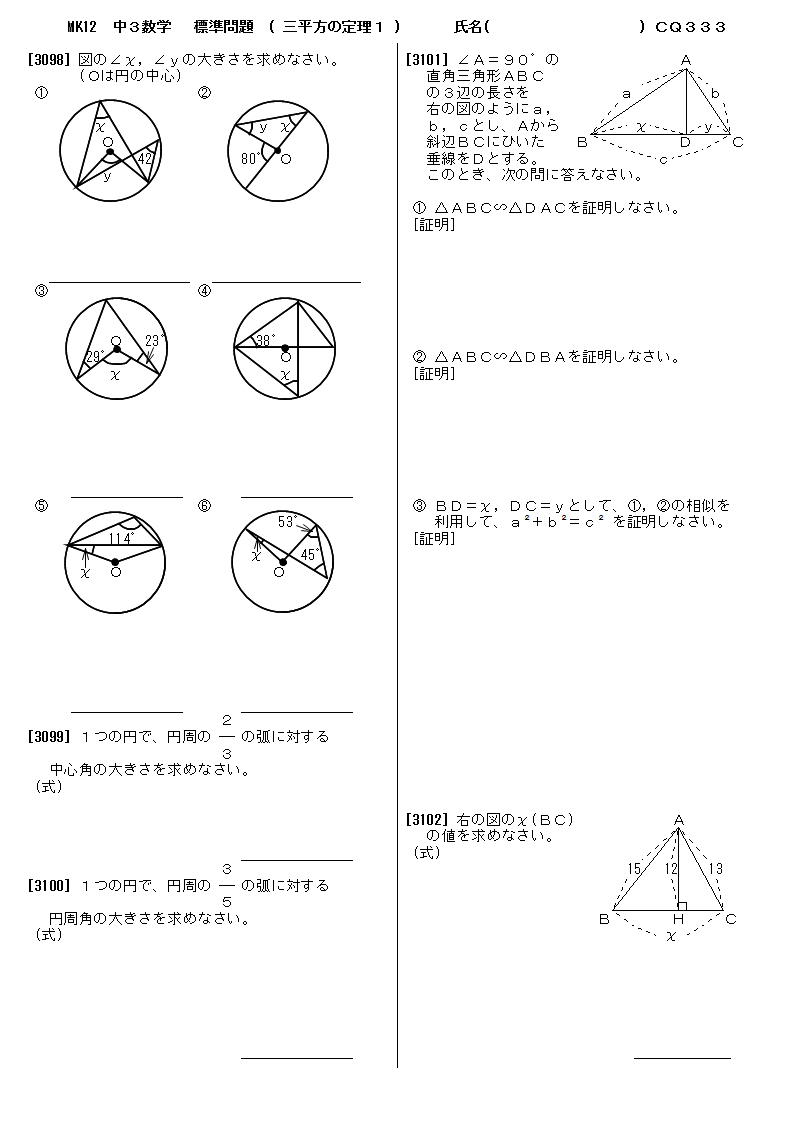
無料 中３数学 標準問題 問題プリント 333 三平方の定理１ 直角三角形

Iflpxjtvx1u1dm

基本 三平方の定理 証明２選 人類の至宝 数学メモランダム

三平方の定理 方べきの定理を用いる 数式で独楽する

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ

三平方の定理の４通りの美しい証明 高校数学の美しい物語

三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

中学受験 ヒポクラテスの定理 学ぶ 楽しむ 世界を泳ぐ ができる数理の世界

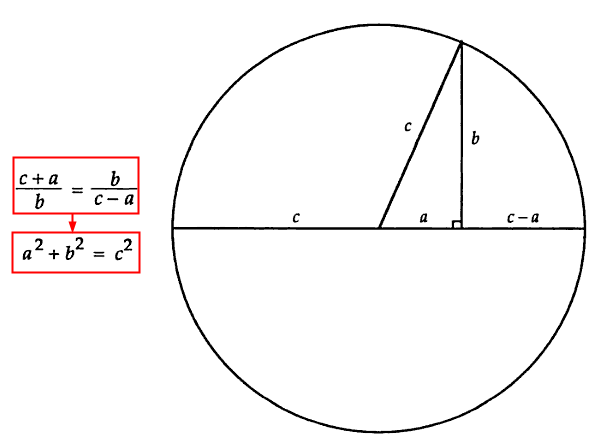
数学の概念 を視覚的かつ美しく表現したグラフィックいろいろ Gigazine

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

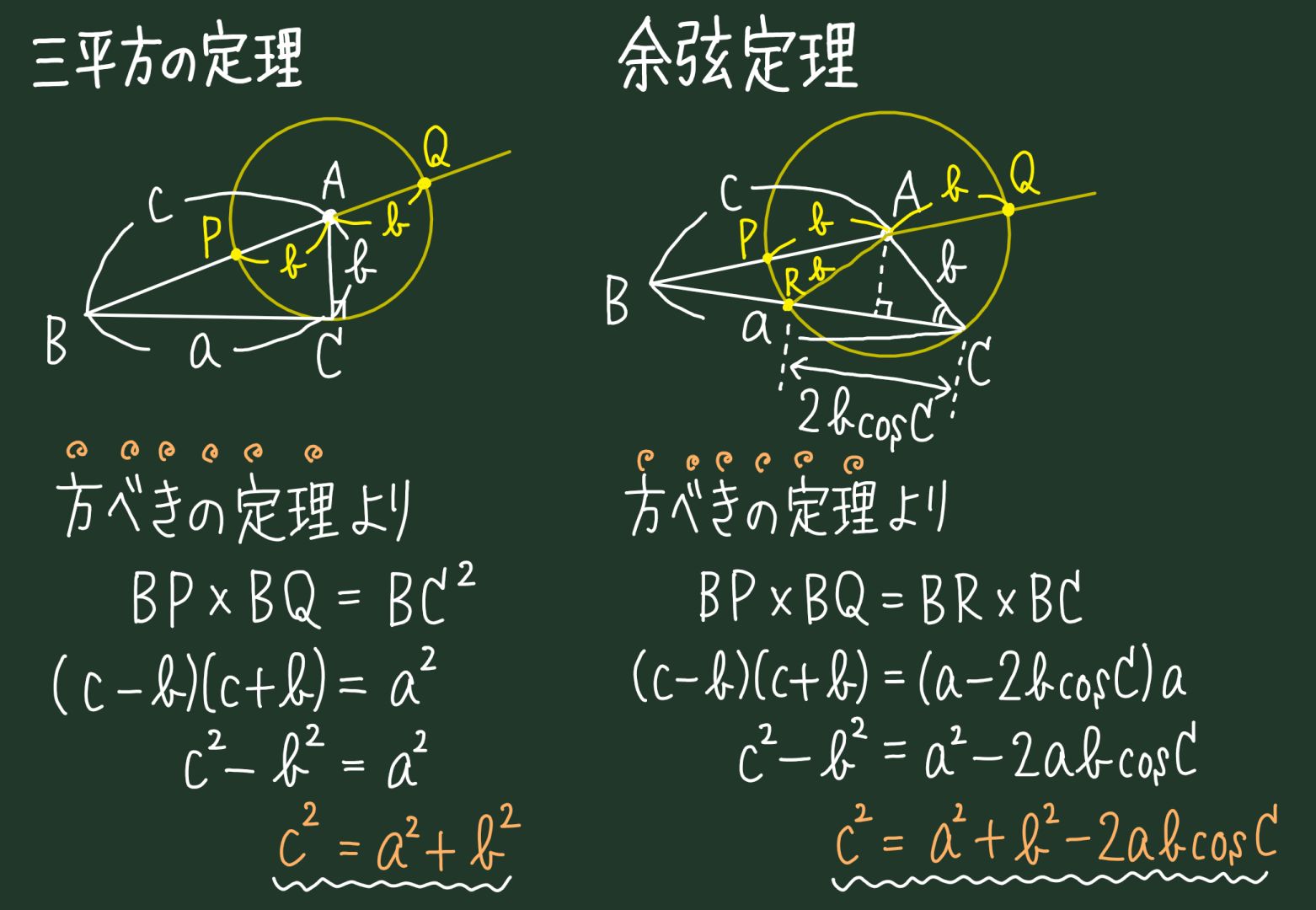
Twitter 上的 すど 忘れないうちに 三平方の定理と余弦定理のほぼ同じ証明 Powered By 方べきの定理 のイラストです T Co Db00rnztzo Twitter

ピタゴラスの定理とその証明

三平方の定理の証明と使い方

中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名

ピタゴラスと三平方の定理 湯川校 清水町 スタッフブログ 個別指導学院ヒーローズ 静岡市 三島市 1コマ1 000円

三平方の定理の証明 直感的に分かる図で解説します 数学fun

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4

三平方の定理を直角三角形二つで証明 Youtube

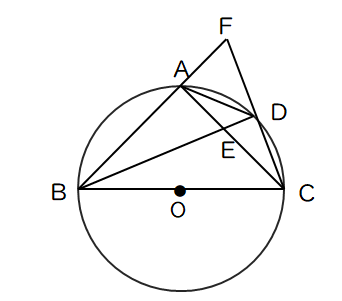
中学数学 よく出る円と相似の融合問題 Pikuu

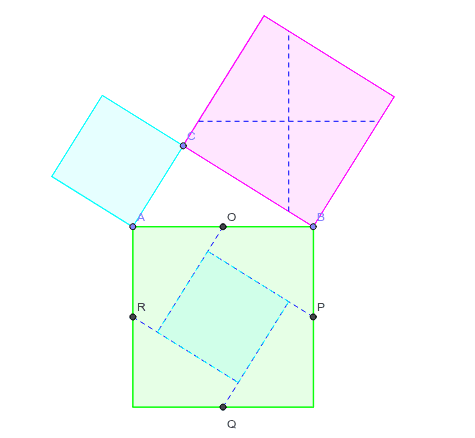
三平方の定理 証明１１ Geogebra

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

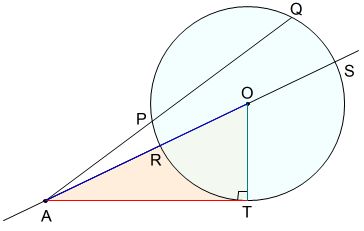
方べきの定理と証明 相似と三平方の定理より Note Board

三平方の定理 無料で使える中学学習プリント

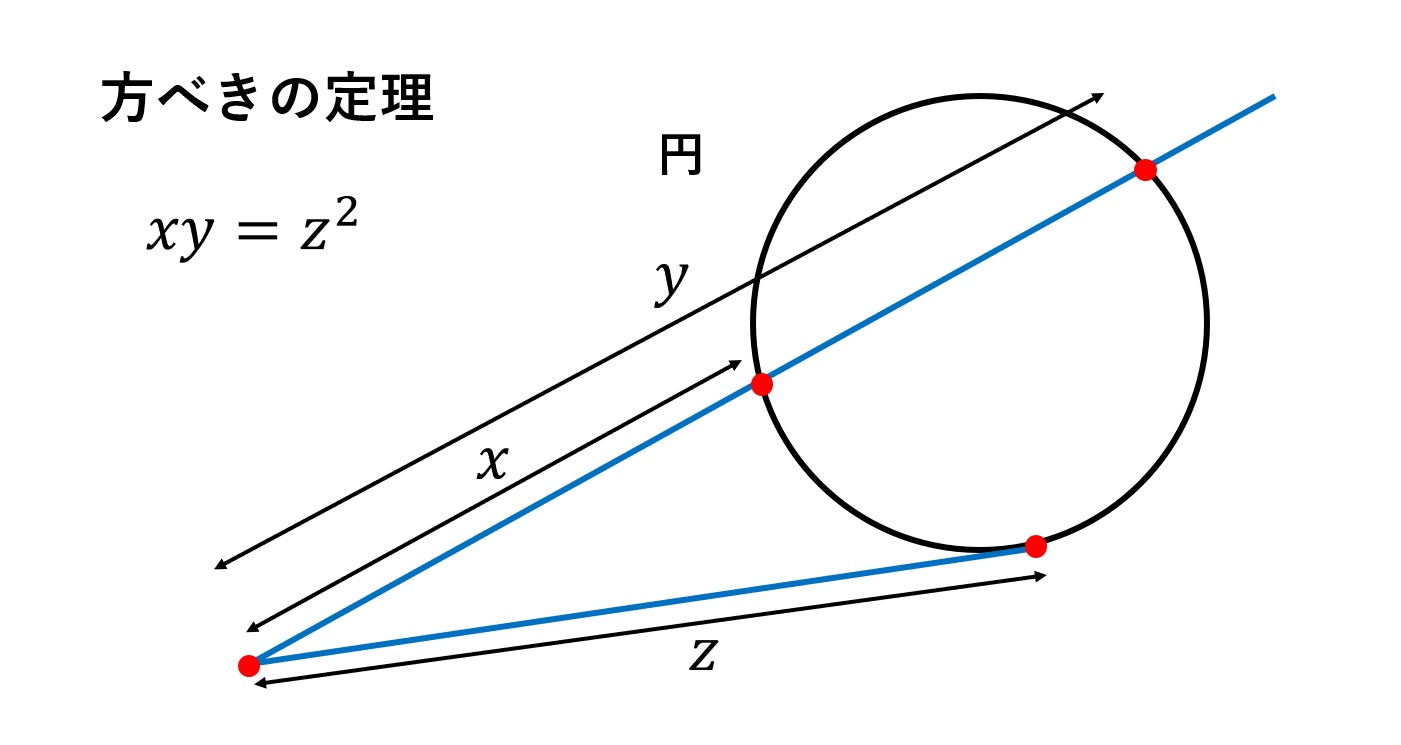
感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

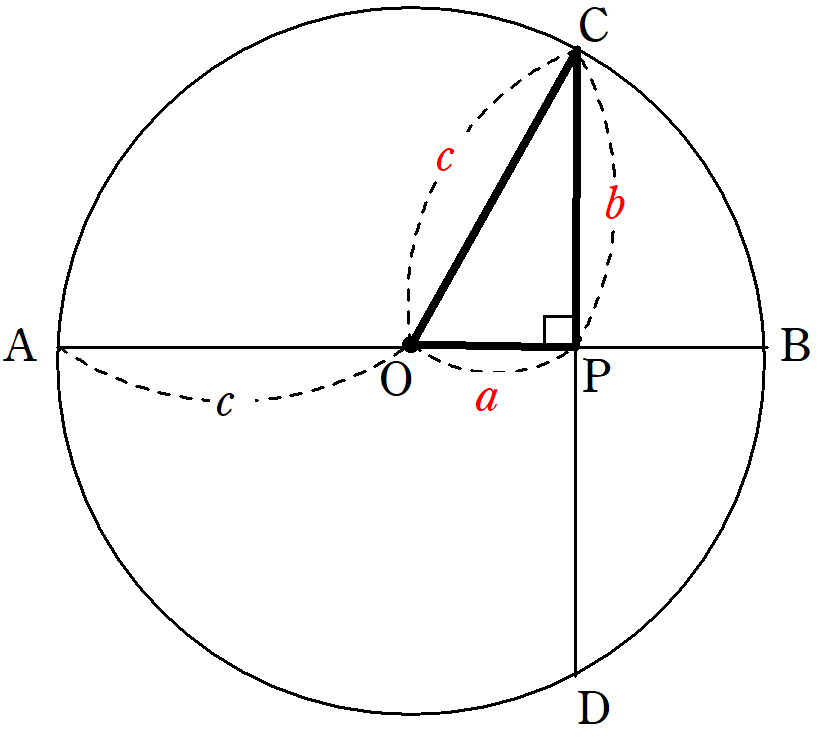
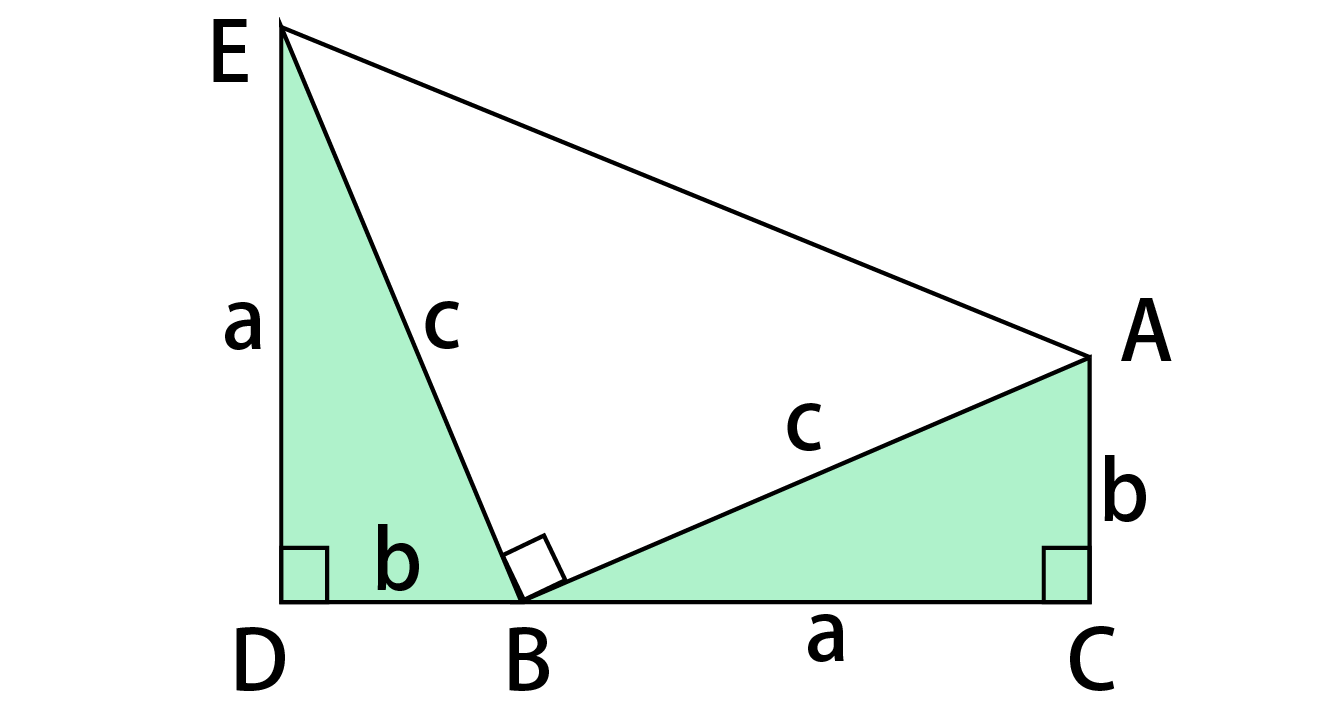
三平方の定理の証明 方べきの定理を利用した２種類の証明をわかりやすく解説 Fukusukeの数学めも

円周率の求め方 三平方の定理で Youtube

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

余弦定理 は三平方の定理の進化版 余弦定理は2つある

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

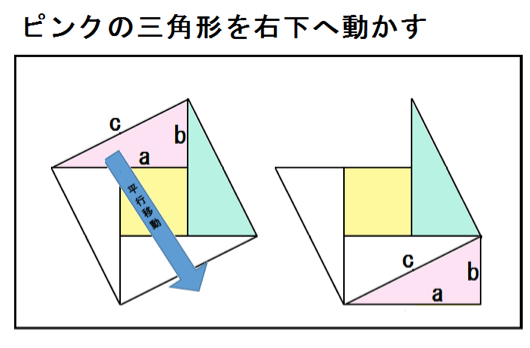
中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく

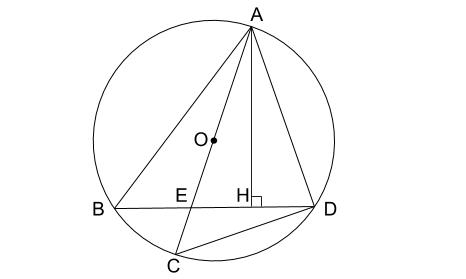
高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su

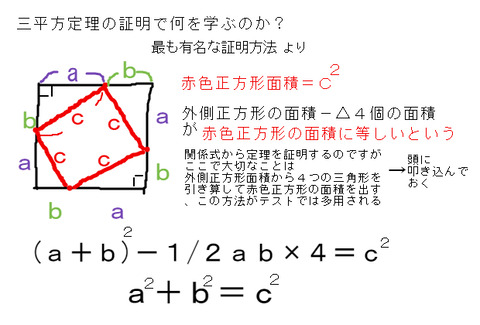
三平方定理の証明内容で最も覚えておくべきこと 中学 数学 理科の復習サイト

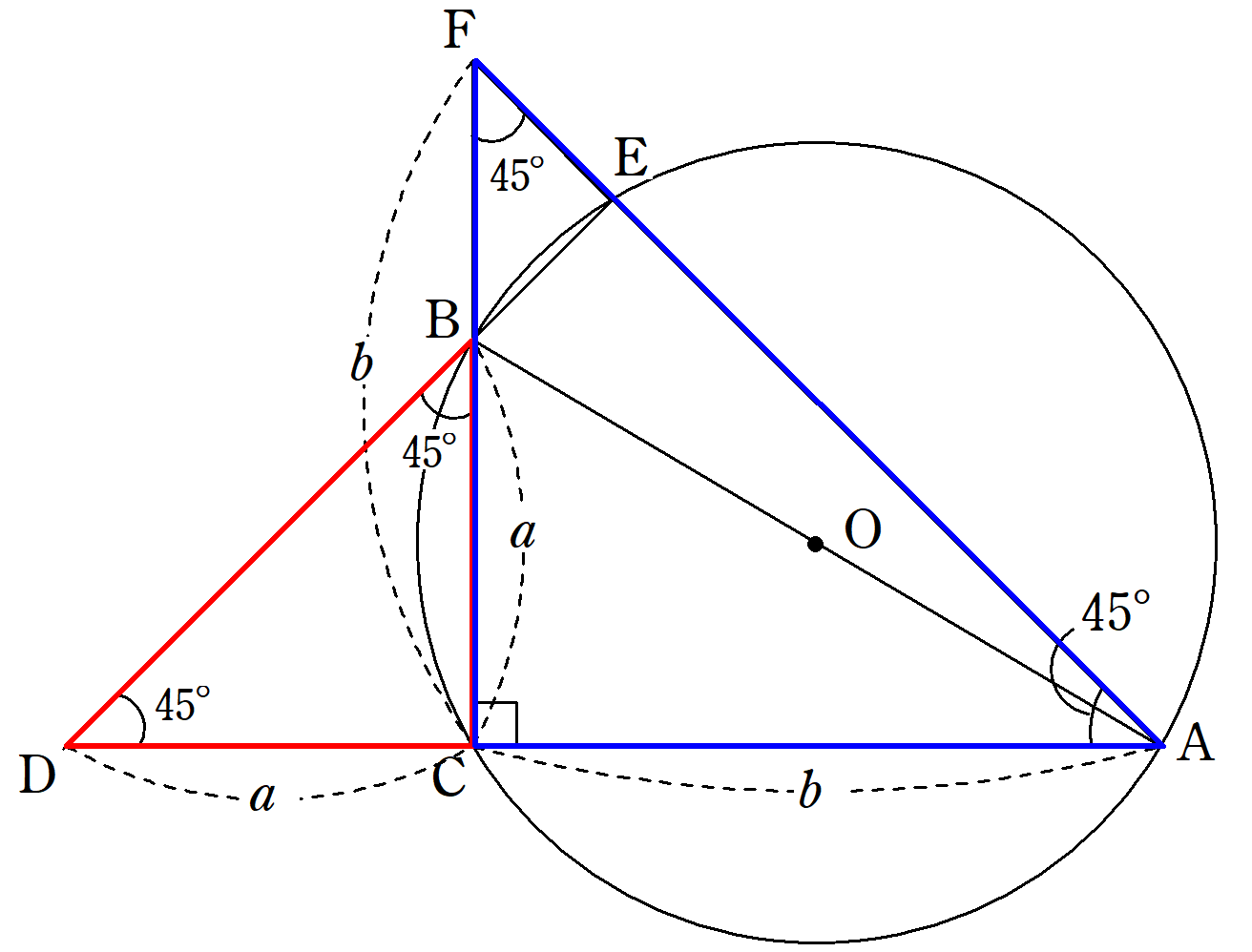
三平方の定理の証明 外接円と直角二等辺三角形を利用した証明をわかりやすく解説 Fukusukeの数学めも

2

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

ピタゴラスの定理 Wikipedia

三平方の定理の最も変わった証明方法はなんですか Quora

三平方の定理 証明

Incoming Term: 三平方の定理 証明 円,