[コンプリート！] 扇形の中心角 求め方 簡単 203648

公式の導き方 扇形は円の一部分を切り取った図形です。扇形の面積は、「 半径が等しい扇形の面積は、中心角に比例する」という性質を使って、円の面積 $\pi r^2$ に$ \frac{\text{中心角}}{360^\circ} $の割合をかけることで求められます。 つまり、1° というのは、円の中心角 360° の360分の1の大き23 中心角なしに扇形 の 表面積に比べて計算が簡単だからです。どのようにして角錐・円錐の体積を求めればいいのでしょうか。 角柱・円柱の体積の計算方法は既に習っています。以下の公式があります。 角柱・円柱の体積 = 底面積 × 高さ;TikTokで扇形中心角求め方関連のショートムービーを探索しよう このクリエイターの人気コンテンツを見てみよう：あきとんとん(@akitonton), あきとんとん(@akitonton), あきとんとん(@akitonton), あきとんとん(@akitonton), 学習塾We'lll(@jukuwelll) ハッシュタグで最新動画を探索しよう：#扇形車

この側面の扇形の中心核の大きさを求める式 がわからないです Clearnote

扇形の中心角 求め方 簡単

扇形の中心角 求め方 簡単-半径と中心角から扇形の面積・円弧の長さ・弦の長さを公式を使って計算します。 半径rと中心角θの値を入力し「扇形の面積を計算」ボタンをクリックすると、扇形の面積・円弧の長さ・弦の長さを計算して表示します。 半径 r： 中心角 θ： 度 ラジアン 半径rが1、中心角θが60°の扇形の面積 前回の続きで円錐の中心角の求め方について解説していきます。考え方は前回と同様ですが、もう1つポイントがあるのでチェックしていきましょう。 hissoritophysmathcom はてなブックマーク はてなブックマーク 中1 中学数学 おうぎ形の中心角 中1数学 中学数学 平面図形

平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト

 360°×(弧の長さ)/(円周)、または、360°×(扇形の面積)/(円全体の面積)円錐の展開図の場合、360°×(底面の半径)/(母線) ナイス！ https//detailchiebukuroyahoocojp/qa/question_detail/q kyn******** kyn********さん 22/2/9 150 どんな問題においてかわからないけど、分度器で測るのが1番速い 1人がナイ 扇形のまわりの長さは、 扇形の弧の長さ＋半径×2 で求められます。 この扇形の弧の長さ＝18×314× ＝14（cm） よって、求める扇形のまわりの長さは 14＋9×2＝3684（cm） 答え 3684㎝ ～平面図形の面積・まわりの長さを求める公式まとめ～ 円の面積扇形の面積の公式は「r 2 θ/2（＝半径×半径×中心角÷2）」です。rは扇形の半径（母線）、θは扇形の中心角（単位はラジアン）です。つまり、r 2 θ/2を算定すれば円錐の側面積が得られますが、θを使わずに側面積が算定できるとより簡単です。

 数学・算数 扇形の中心角の求め方 はじめまして biglobeなんでも相談室 初投稿です(^^)w 扇形の中心角の求め方を 恥ずかしながら忘れしてしまったので 学生の私が 簡単に理解することが 底面の半径が3cmなので、円周＝直径×\(π\)＝6\(π\) cm となります。底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6\(π\)cmです。 そこから、半径12cm＆孤の長さ6\(π\)cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。 まずは同じ半径(3㎝)を持つ円の面積を求めます。 3×3×π＝9π あとは公式に当てはめていくと

扇形の中心角を求める問題です。 扇形の面積が分かっているときは、 円の面積と扇形の面積を比べて、扇形が何倍になっているのかを調べます。 扇形の弧の長さが分かっているときは、 円の周の長さと扇形の弧の長さを比べて、扇形が何倍になっているのかを調べます。 扇形の割合が分かっ①半径と、弧の長さが与えられて中心角を求める問題 ②半径と、面積が与えられて中心角を求める問題 これ以外のパターンはありません^^ これです⇩これを覚えましょう 橘 美采 約5年前 ありがとうござい 扇形の中心角を求める式の作り方ですが、こう考えましょう。 中心角/360=弧の長さ/円周 この式は円の中で扇形の中心角が占める割合と、円周の中で弧が占める割合が一緒という意味です。 よって 中心角=弧の長さ/円周×360 の式がなりたちます。

扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg

扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち

 このブログは、はかせのワンオペです (*' ') 扇形の中心角を求める公式 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね はかせちゃん はかせOfficial 中心角の求め方概観 公式 円すいの中心角の求め方は、 \(x=\displaystyle \frac{ 360r }{ l }\) でしたね。 この公式に\(r=2\)、\(l=8\)を代入して、\x=\displaystyle \frac{ 360×2 }{ 8 }\よって、\\style{ colorred;弧の長さ は、 r θ と表されるので、中心角に比例します。 一方、 弦の長さ は、 2 r sin ⁡ θ 2 と表されるので、中心角には比例しません。 また、中心角が等しい場合、 弧の長さ は 弦の長さ よりも長いです。 どちらも、 0 ∘ ≤ θ ≤ 180 ∘ の範囲では

扇形 中心 角 求め 方 おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う Tmh Io

3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ

中心角の割合を求める 36/360 = 1/10 円の面積を求める （半径×半径×円周率） 5 × 5 × π = 25π おうぎ形の面積を求める 25π × 1/10 = 25π cm 2 弧の長さを求める場合も考え方は同じで、中心角から割合を求め、円の円周に割合を掛けて弧の長さを求めます。 円周を求めるときには、直径で求める点に注意してください。 おうぎ形の弧を求める公式 弧の長さ=円周×中心角の割合 半径10cm、中心 直 径 直 径 × 314 = 3 × 2 × 314 = 14 c m おうぎ形の中心角を求める おうぎ形の弧の長さ は、 円の円周 と同じ長さなので 14 c m また、このおうぎ形の元となった円 (半径 5 c m )の円周の長さは、 5 × 2 × 314 = 314 c m おうぎ形の弧の長さと、元の円周 (半径 5 c m )の長さを比べると 14 ÷ 314 = 3 5 よって、おうぎ形は円の 3 5 であるから、求める中心角は 360 ∘ × 3 5 中心角を \(x\) とすると、扇形の面積公式を利用し $$\pi \times 6^2\times \frac{x}{360}=12\pi$$ という方程式を作ることができます。 あとは、この方程式を解いていくだけです。 $$\frac{x}{10}=12$$ $$\frac{x}{10}\times 10=12\times 10$$ $$x=1°$$ よって、扇形の中心角は1°となります。

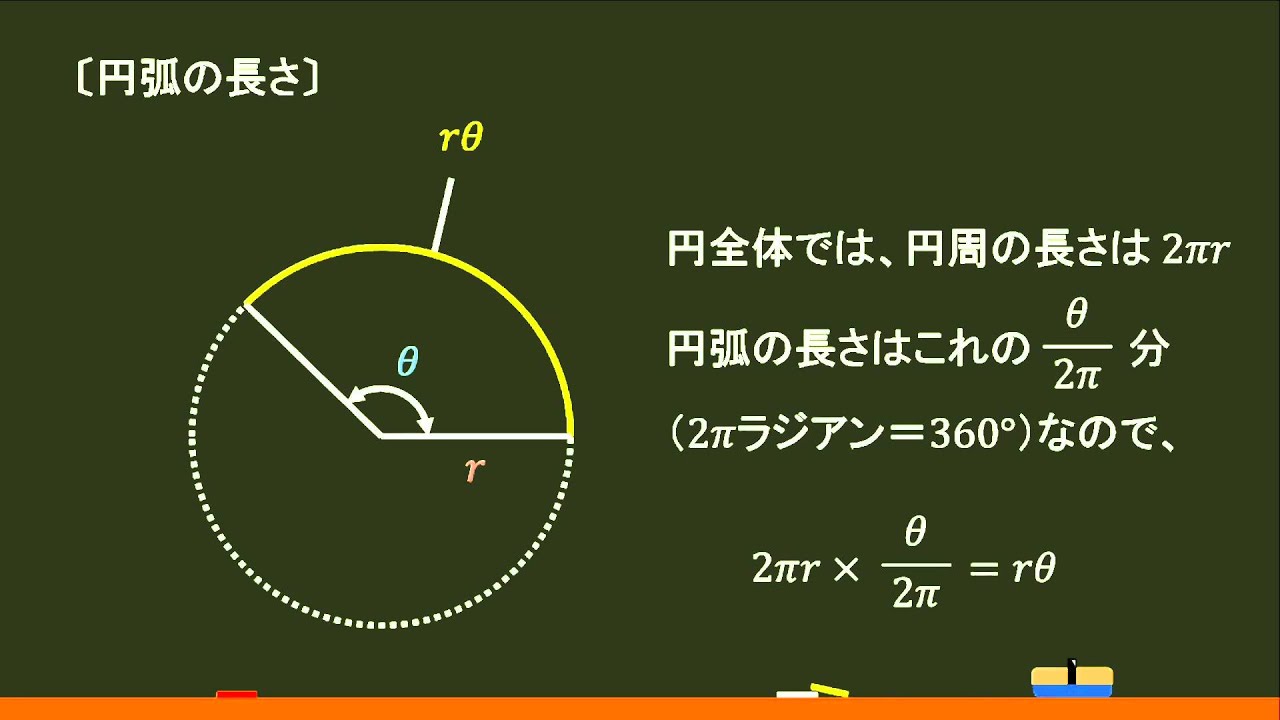
数学 三角関数 円弧の長さと扇形の面積 弧度法 オンライン無料塾 ターンナップ

図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師

 弧 の 長 さ 半 径 中 心 角 弧 の 長 さ = 半 径 × 2 × 314 × 中 心 角 360 ∘ 中心角のわかっている、おうぎ型の 面積 を求める公式 面 積 半 径 半 径 中 心 角 面 積 = 半 径 × 半 径 × 314 × 中 心 角 360 ∘ 面積を2倍 にすると 面 積 半 径 半 径 中 心 角 面 積 × 扇形の中心角の求め方で、πが入っていました。求めると、 π°となりますよね？ この公式は合っていますか？ またπは必要ですか？ ★円錐の表面積★簡単な求め方とその理由を解説するぞ！ 側面である扇形の面積を求めようとすると、扇形の公式から分かるように 中心角が必要になります 扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターン を見てみてね ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線 こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど！ 何を求めるのも公式だよりってなると "応用問題に対応できない" , "覚える数が多すぎて忘れちゃう" ってことになるから

扇形 中心 角 求め 方 数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 Luismiguel Pt

円錐の表面積 中心角を求める問題を丁寧に解説 数スタ

おうぎ形の中心角の求め方 演習問題で理解を深めよう！ 円とおうぎ形の公式 まとめ; 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値（半径）を求めることができます。 この 扇形の弧の長さは、同じ半径をもつ円の円周の長さに中心角の割合をかければ求められます。 扇形の弧の長さの求め方 \begin{align}\text{(扇形の弧の長さ)} = \text{(円の円周の長さ)} \times \text{(中心角の割合)}\end{align}

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

扇形の中心角の求め方を教えてください 中心角の求め方は２通りのパタ Yahoo 知恵袋

扇形の弧の長さ（ l ength） π 円周率（= 314） r 円の半径（ r adius） x° 中心角 公式の導き方 この公式は暗記するようなものではなく、意味を理解することに意味があります。この公式の意味は、円の面積に「360° に対する中心角の割合をかける」ことに 扇形の面積の求め方は、半径と中心角から求める方法が一般的です。 半径と中心角から扇形の面積を求める 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 頭の中に 扇形の中心角の求め方 はじめまして biglobeなんでも相談室 初投稿です(^^)w 扇形の中心角の求め方を 恥ずかしながら忘れしてしまったので 学生の私が 簡単に理解することが出来るような 扇形の中心角の求め方(公式）を 教えて下さい(~_~;) ベストアンサー 数学・算数;

中学１年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

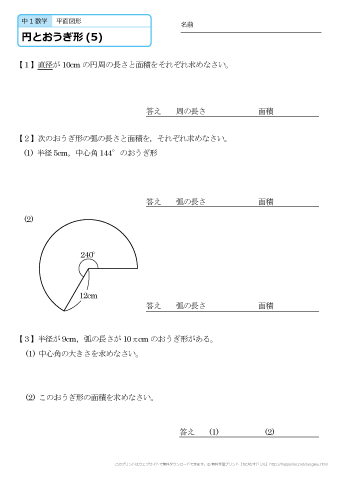
中学１年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

 ベストアンサー：弧の長さと、半径が与えられているはずです 円弧の長さは中心角に比例 半円は扇形の中心角が180度なので 中心角／180＝円弧の長さ／円周率×半径 ということ先ほどと同じように、円の円周は直径×πなので、 2×5×π＝ 10π となります。 ここで中心角を aというアルファベットにして考えていきます。 もとの円の一周の角度は360°なので・・・ このような公式となります。 もとの円の円周×a/360°＝おうぎ形の弧の長さ これを計算すると a = 216°となります。 したがってこの問題の中心角は 216° です。扇形 ～弧の長さ、半径から中心角を求める～ 作者 Enpitsu さん 実行数

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

おうぎ形の弧の さと 積の求め方 中学受験プロ講師ブログ

 扇形の部分が円の「何分の1」なのかがわかれば簡単に解くことができます。 つまり、円は360度なので、扇形の中心の角度がわかれば以下のような公式に当てはめるだけで問題を解くことができます。 おうぎ形の弧の長さ ＝ 直径 × 円周率 × 中心角 ÷ 360 「扇形の中心角の求め方」の公式ってチョー便利。教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。たとえば、半径 4 、弧の長さが 6π の扇形があったとしよう。この「扇形の 扇形の中心角と弧の長さは比例します。 角度が 「 °」であれば、 弧の長さ＝円周×中心角÷360 という式になります。中心角を求める形にするなら 中心角＝弧の長さ÷円周×360 円周は半径から出せますから とも表せます。

中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ

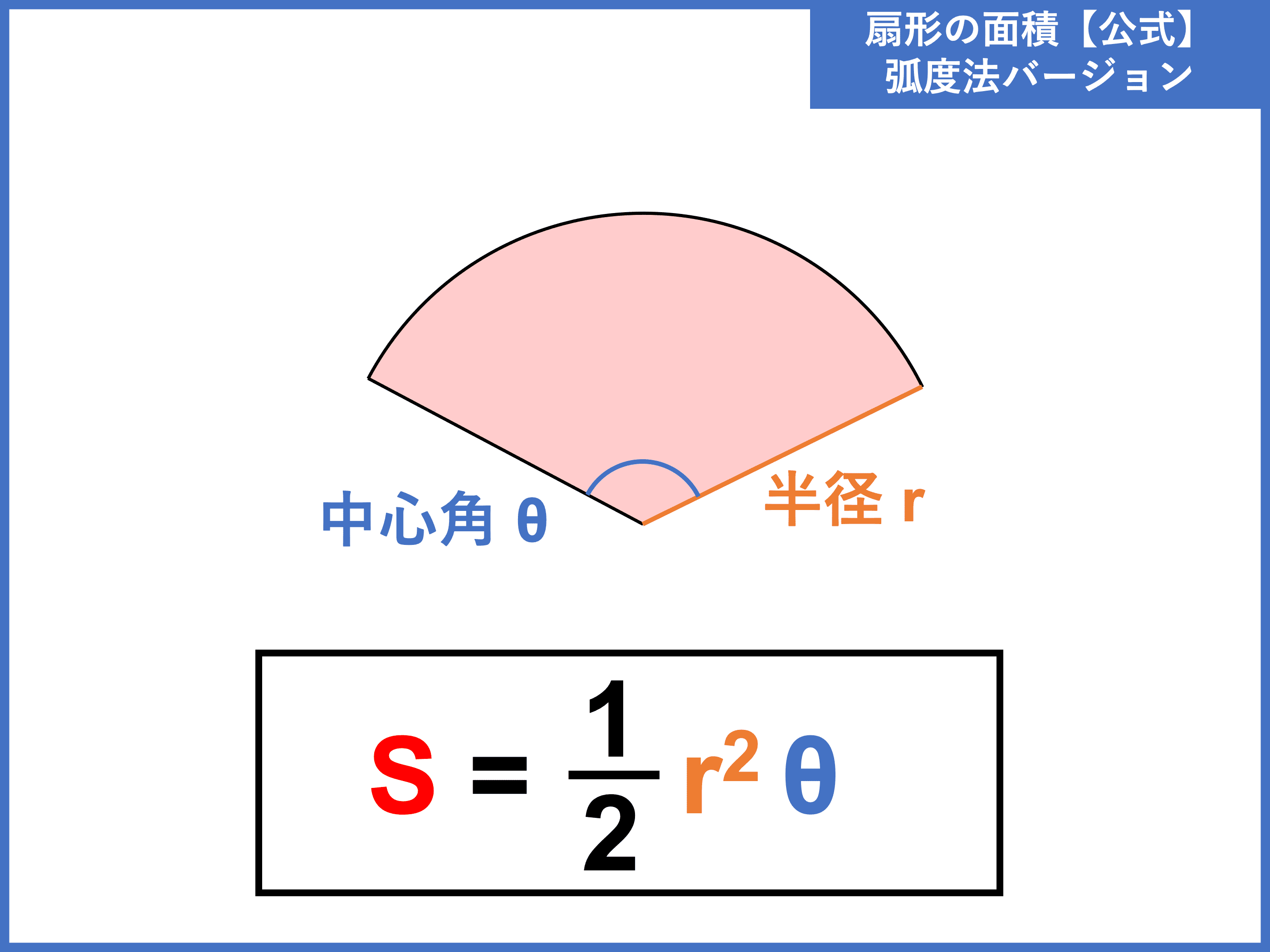
扇形 中心 角 求め 方 中学数学 円錐の 母線の長さ がわかる2つの求め方

 角度の求め方 超簡単な方法教えます！ 扇形の中心角をX°、弧の長さをL、半径をrとすると、 Xは180L/πr になる。 →つまり！ 扇形の「半径」と、「弧の長さ」が分かれば「中心角」を求めることが出来る！ ！

円柱の表面積の求め方

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

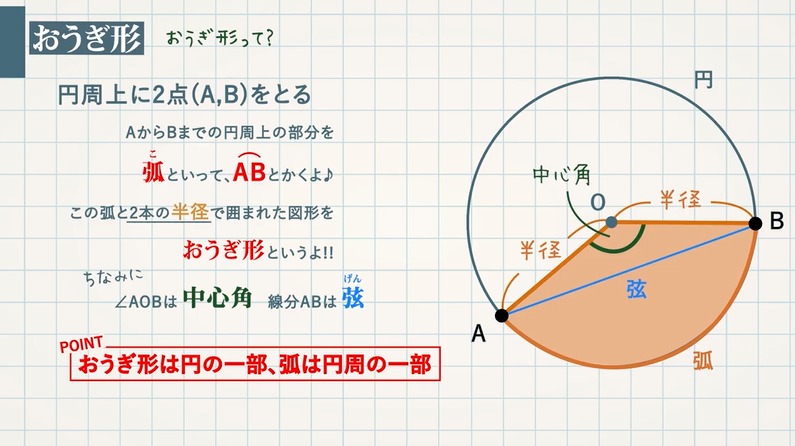
おうぎ形まとめ 弧と面積の求め方 教遊者

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

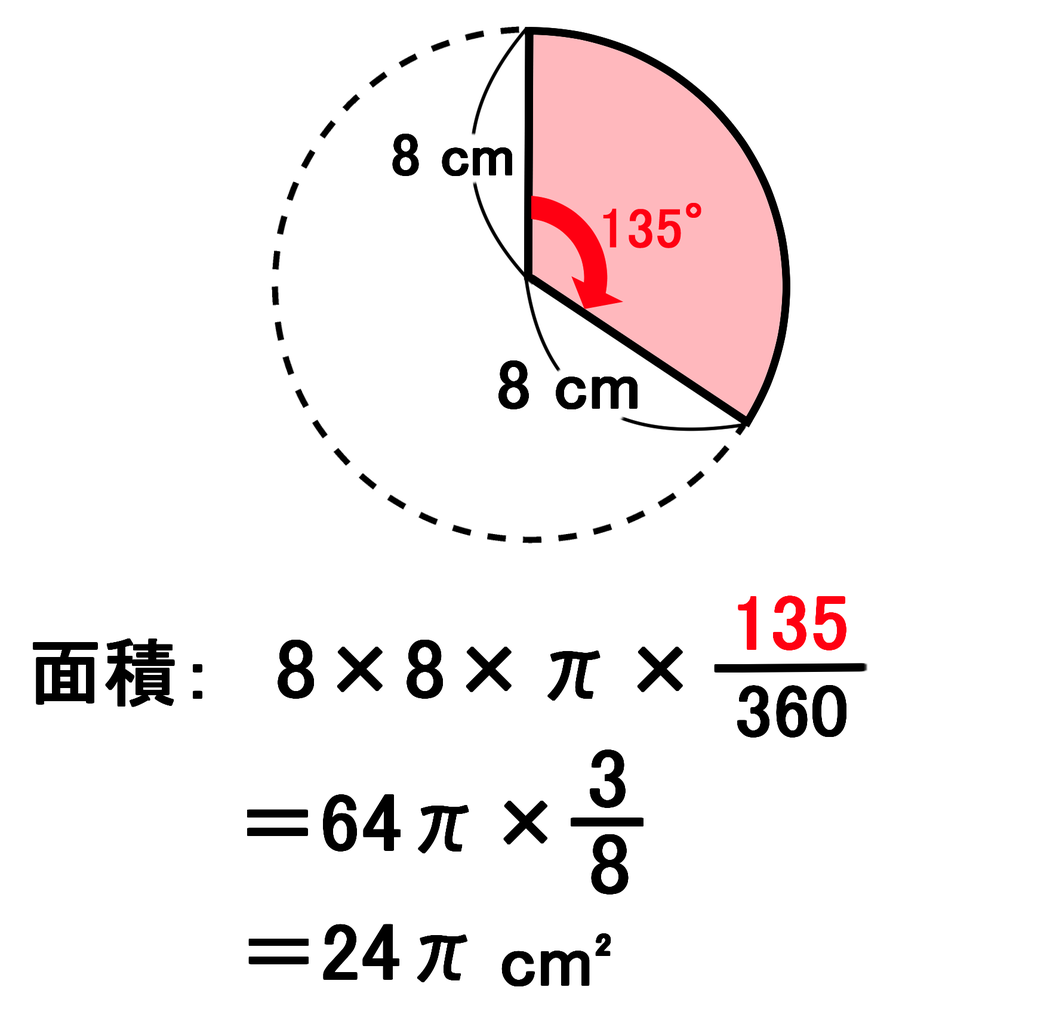
おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学

この周の長さが12p 12 Cm なのですが分からないので解き方を教えてくだ Clearnote

3

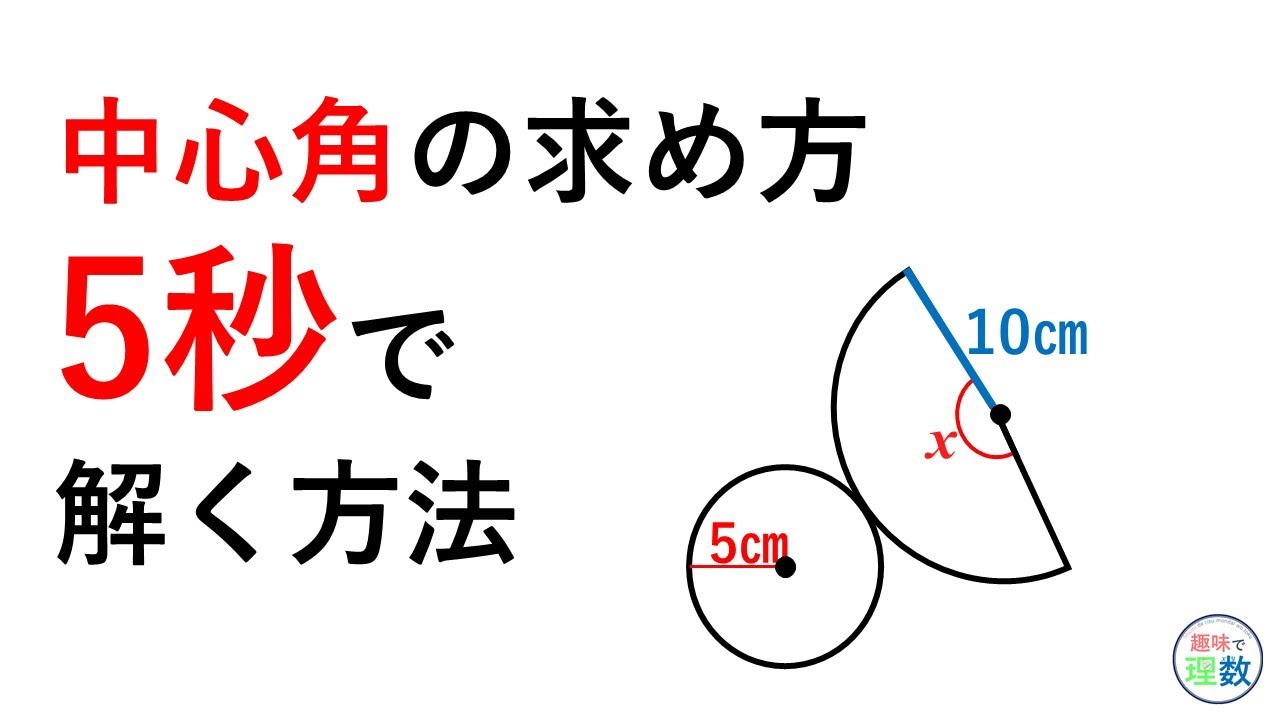
おうぎ形の中心角の求め方 Youtube

扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学

扇形 中心角 公式 学び 教科書 勉強

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト

問題の 2 おうぎ形の中心角の求め方の解き方を教えてください Yahoo 知恵袋

半径4cm面積6pcm の扇形の中心角の求め方を教えてください Yahoo 知恵袋

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

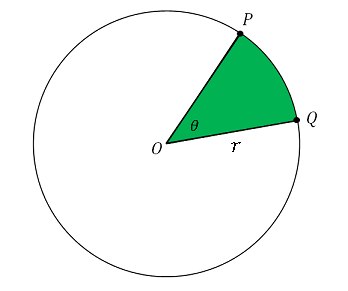
扇形の弧の長さと面積 Excel Vba 数学教室

おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

半径4cm 面積10pcm の扇形の中心角の大きさを求めなさい Yahoo 知恵袋

1

おうぎ形の中心角の求め方 Youtube

扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト

扇形の弧の長さの求め方 公式と計算例

扇形の面積の求め方 公式と計算例

扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー

円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張

円 扇形 の面積 周や弧の長さの公式 数学fun

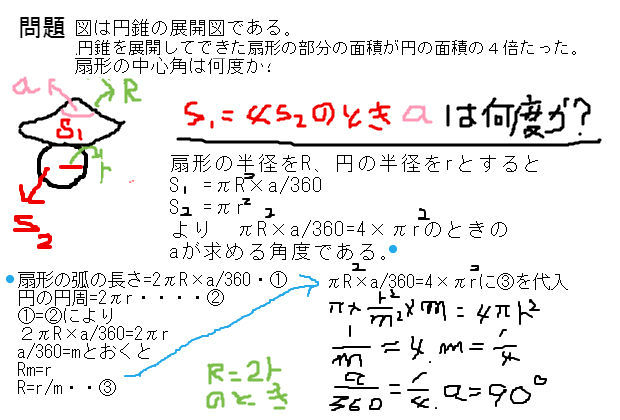
扇形と円錐に絡む問題を速解する必須知識と実践問題 中学 数学 理科の復習サイト

なぜ おうぎ形の面積は１ ２ 弧の長さ 半径 なのか を説明します おかわりドリル

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題

扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

1分でわかる 扇形の中心角の求め方 Youtube

図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 小学生 算数 面積 勉強法

扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト

扇形 の 中心 角 公式

この側面の扇形の中心核の大きさを求める式 がわからないです Clearnote

3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ

この 中心角の求め方を教えてください １ の方です Clearnote

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

中学数学 扇形の中心角の求め方３パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室

扇形 中心角 公式 学び 教科書 勉強

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

中１ 数学 空間図形９ おうぎ形の公式 １７分 Youtube

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

1

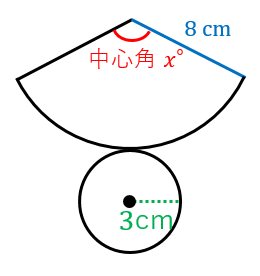
円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学

表面積の問題で 中心角の求め方が分からず答えを見たんですが 説明文の意味がわ Clearnote

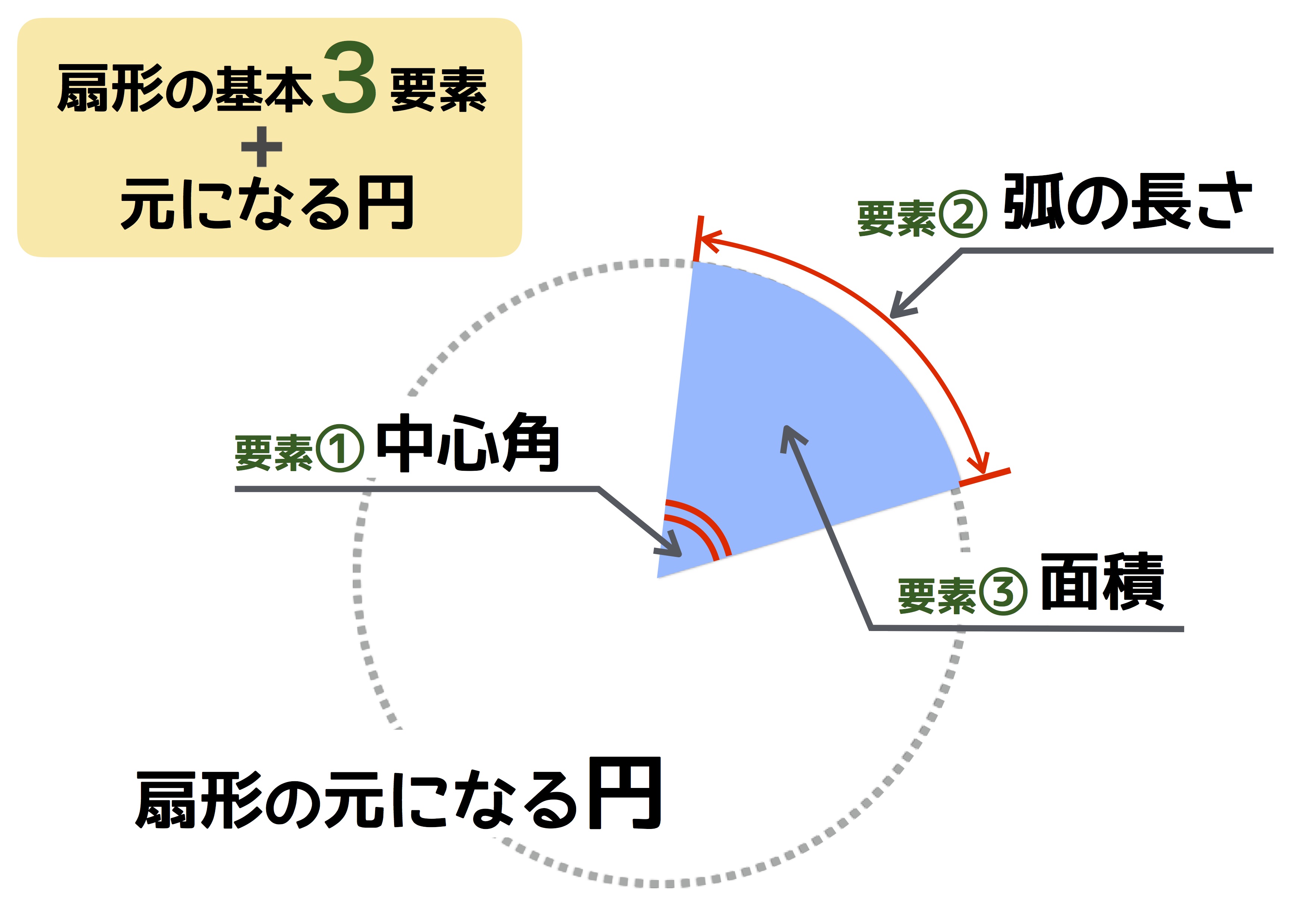
扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ

扇形の中心角の求め方を教えてください Clearnote

扇形面積求め方 扇形の弧の長さと面積 小學 中學數學での平面図形の Txfs Co

楽しい数学 中心角の裏ワザ 塾のおしごと

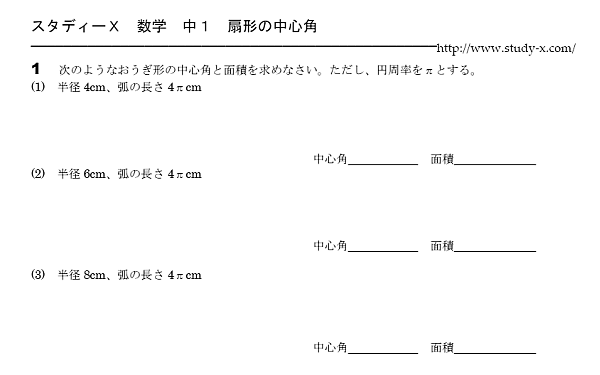
扇形の中心角 無料学習プリント教材

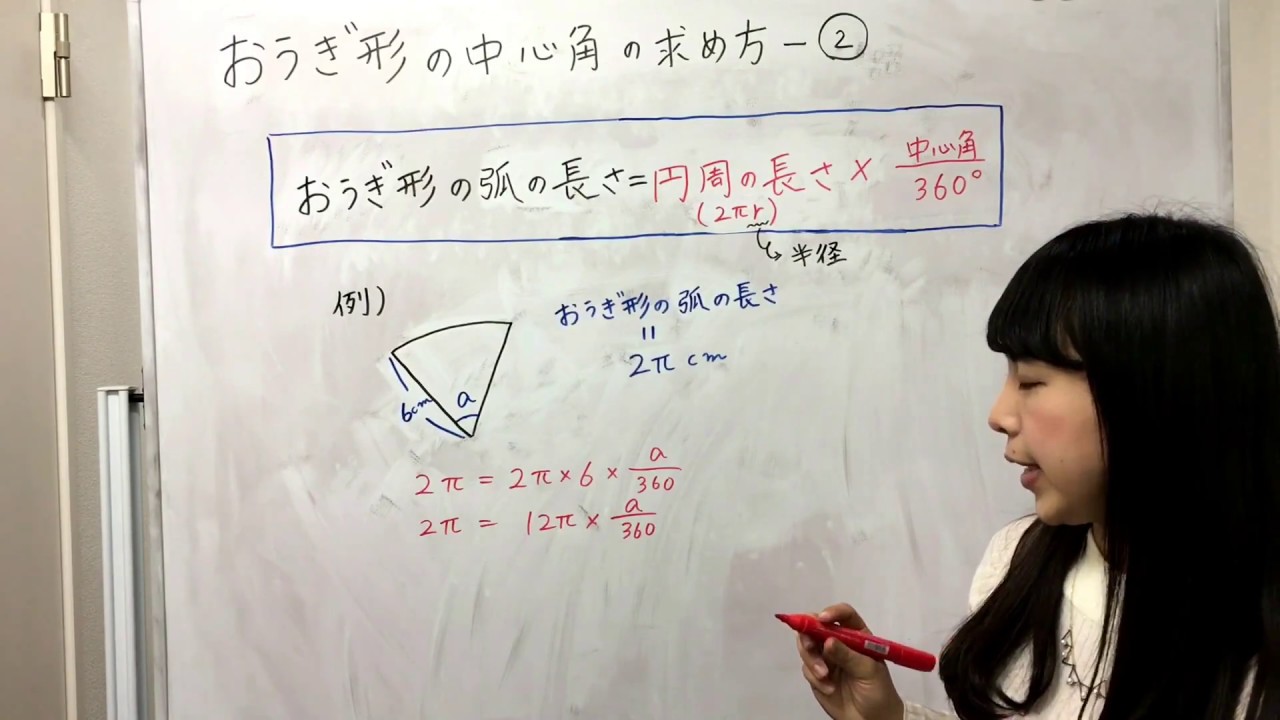
中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube

おうぎ形 半径の求め方 数学の記録

扇形の弧の長さと面積 計算ドリル 問題集 数学fun

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube

扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw

この問題の求め方がわかりません 中心角45度の扇形からどこをひけばよいのでし Clearnote

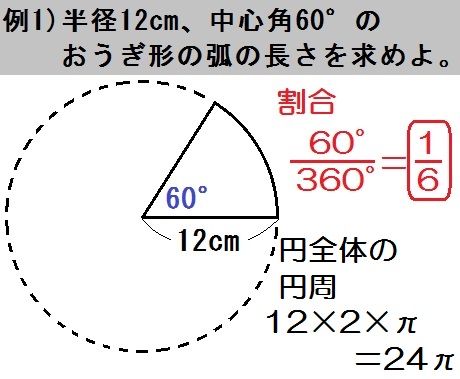
中学数学 平面図形 のコツ 円とおうぎ形

半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋

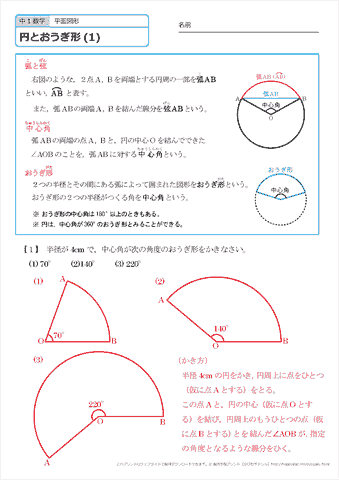
中学１年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

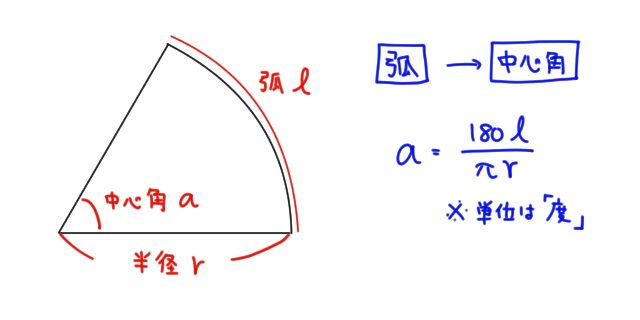
おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張

おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学

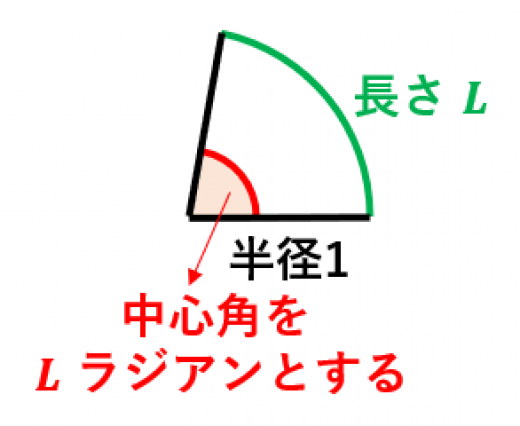
弧度法の意味と度数法に対するメリット 高校数学の美しい物語

扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア

扇形面積公式扇形の面積と公式 Enhti

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

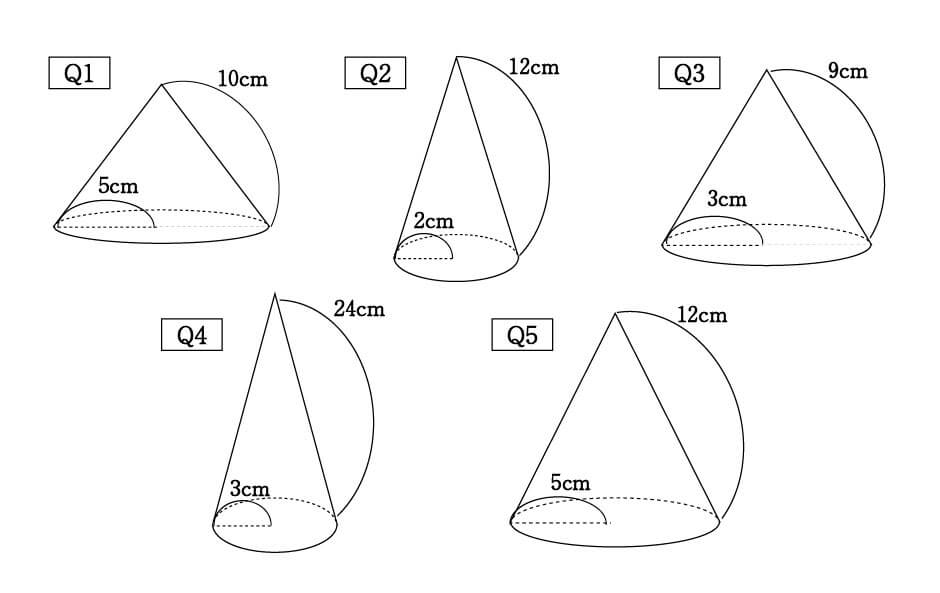
数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち

弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか

中心角40度 弧の長さ２pｃｍの扇形の面積中心角３０度 弧の長さpｃｍの扇形 Yahoo 知恵袋

弧度法とは 度数法との違いと表 求め方 理系ラボ